Efficient AI

One of the great benefits of lockdown for me is the time I have to catch up on some of the papers released that are not directly related to my day to day work. In the past week I’ve been catching up on some of the more general outputs from NeurIPS 2020. One of the papers that really caught my eye was “Ultra-Low Precision 4-bit Training of Deep Neural Networks” by Xiao Sun et al.

It’s no doubt that AI in its current form takes a lot of energy. You only have to look at some of the estimated costs of GPT-3 to see how the trend is pushing for larger, more complex models with larger, more complex hardware to get state of the art results. These AI super-models take a tremendous amount of power to train, with costs out of the reach of individuals and most businesses. AI edge computing has been looking at moving on going training into smaller models on edge devices, but to get the accuracy and the speed, the default option is expensive dedicated hardware and more memory. Is there another way?

Back in 2018, I gave a talk at Minds Mastering Machines in London about a topic close to my heart, Making AI Efficient. Performance of the human brain is many orders of magnitude more efficient in energy usage alone than GPUs and TPUs. As GPUs have got more powerful, the energy consumption has scaled accordingly. Even the new GTX 3080s are recommended to have 750W PSUs. We are getting processing power improvements but for no real gain in power efficiency. Added to this, there is no pressure on us as a community to code our models efficiently to make the most of what we have. We just buy more GPUs and add more RAM alongside more data.

One of my favourite quotes is attributed to Ernest Rutherford and is “We haven’t got the money, so we have to think”. When you are limited in your resources, you are forced to be more creative in how you use them or you will not progress. I see many businesses who look for the “easy outs” – we need better data, we need better hardware, rather than step back and look at the problem differently to innovate rather than evolve.

Back in 2018 I certainly didn’t have the answer, and could only provide some ways of thinking to the community to help them code their models more efficiently. I had started playing around data encoding methods to try and get more data into my batches while still using the 4G on board RAM of my laptop GPU, but definitely hadn’t found anything that maintained accuracy.

Fast forward a few years, ¹ and the paper by Xiao Sun. I was very excited to read this, and I’d recommend that you take a look at it. Building on work in low precision arithmetic that had been developed in 2018 and 2019, and also work applying these results to various deep learning methods, they took these ideas a step further to 4 bit format, end to end solutions and retain benchmark accuracy (with a negligible loss) with significant hardware acceleration. Part of this work is a new 4 bit format that uses logarithms². Rather than 4 bits giving a range of 0-15 (or signed), each bit represents a subsequent power of 10 giving . This is the sort of simple idea that happens in mathematics that is completely obvious to everyone only after someone has pointed it out.

There are some nuances in rounding to force values into one of the bit positions and there is also no space for infinity or NaN values, which means that a lot more care must be taken with development of the code to avoid hitting these limits. As you can see on their experiments with ResNet18 (ImageNet)³, their approach had the range to represent most gradients and they minimised their mean squared error by using a rounding factor of 1.6 to force the gradients into the bit positions.

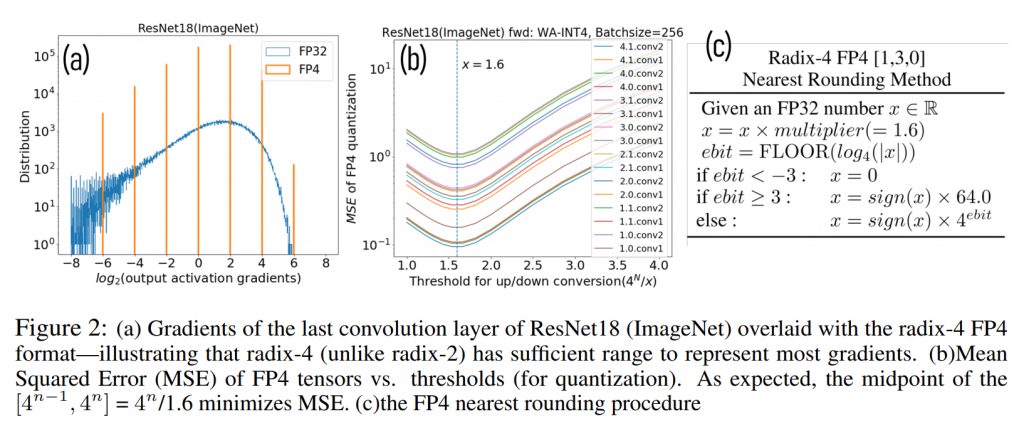
In binary architecture, this looks like the limit as a 2 or 3 bit approach wouldn’t have the range for the activation gradients needed⁴. They also implemented different scaling factors per layer to preserve as much accuracy as possible and prevent under/over flows, absolutely critical to keep the values “honest”. This approach also ensures the accuracy is within 0.5% of the baseline using 32 bit values.

There are further mathematical tricks they employed to ensure that the gradients for back propagation and the weight activation gradients are as accurate as possible by using and value formats as a two phase quantisation rounding at each level. This is a great use of the bits available to maximise information storage. Where the rounding direction is opposite between odd and even then the errors cancel out, in all other scenarios, each phase has a 50% chance of having a smaller error than the other.

These three innovations result in a 4-bit implementation of ResNet18 that could achieve ~1% accuracy loss. Different implementations and architectures had higher losses so there is still work to be done, generally the larger networks performed worse in 4-bit, which is not unexpected with the loss of numerical precision. The authors include some notes to this and particularly highlight “task-specific robustness studies”⁵ to validate this approach for “real applications” and I completely agree. These results are very promising, but more work is needed before we see a “4-bit Tensorflow” (or equivalent) implementation for general use.

This work was also only a simulation of 4 bit architecture and IBM are working on 4bit hardware to support this. I must admit to having a slight problem with this. We already have GPUs and TPUs as application specific hardware (ASICs) and while I fully support the efficiency of these networks, I worry that this new hardware would not be commercially palatable as it would be hyper-specific.

Ideally we should have machines that can support multiple task types and use their data registers effectively. Historically, integer mathematics has been faster on computers that calculation with floating point. However, in python, integers are of unlimited size while floats are fixed, meaning that floating point arithmetic can be faster! The C programmer in me wonders if there is a way of leveraging some of the research of Xiao Sun into a low precision numeric library, allowing ML researchers to continue to write in python but have the benefit of the speed and memory efficiencies this approach provides. This feels like another research project in itself!

I find this research for lower resource machine learning fascinating and very much worthy of time and money. There are benefits for many edge devices⁶ if we can get this right, as well as decreasing the energy consumption of larger models on servers by far more efficient use of the resources on the chips. In this case, with lots of small nibbles rather than a large byte 😉